안녕하세요?
드디어 각각의 period별로 결과를 다시 얻는데 성공해서, 이제 전체적으로 비교를 해 봐야 하는 시간이 오기는 왔습니다. 물론 이제까지 했는 것이 있기는 있기 때문에, 아무튼 각각의 period별로 비교를 해봐야 하는 시간이 오기는 왔습니다. 일단 이 데이터 분석이 끝난 다음에는 RSI지수를 가지고 했는 결과도 분석에 들어가 보고자 합니다.

먼저 위 스크린샷에서 볼 수 있는 것처럼, 일단 한가지 기묘한 것은 10분봉 캔들챠트 데이터 베이스를 가지고서 표준편차에 배수를 전혀 주지 않았을 때의 결과인데, 일단 이익의 평균은 period가 줄어들수록 증가하지만, 그 이상으로 어찌도니 것인지 더 많은 손해의 평균을 보여주고 있습니다. 다만 이럼에도 불구하고 이익의 표준편차가 줄어든다 = period가 줄어들 수록 일정한 양의 수익을 얻을 수 있다는 것을 의미하기는 합니다.

그리고 나서 다음으로 한번 30분봉 캔들챠트 에서 얻은 결과를 가지고 각각의 period별로 한번 정리를 해 보았습니다. 일단 여기서도 가장 적은 period에서 이익의 평균이 컸고, 점점 이익의 표준편차가 내려간다 = 일정한 양의 수익을 낼 수 있다는 것을 의미하고 있습니다. 다만 이러고도 손해의 평균이 증가한다는 점에서 종목 선정에 중요성이 커진다는 것을 알 수 있습니다.
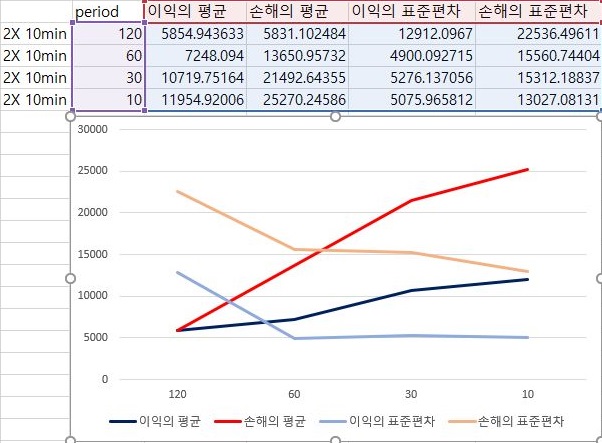
그리고 나서 다음으로 할 수 있는 것으로는 10분봉 캔들챠트 데이터 베이스에서 얻은 결과를 가지고서, 한번 표준편차에 2배수를 해주는 결과를 분석해 보고자 합니다. 여기서 역시나 얻을 수 있는 결과로는 역시나 period가 줄어들면 줄어들 수록 이익의 평균은 손해의 평균이 늘어나게 되는데, 이를 어떻게 해석해야 할지는 모르겠습니다.

다음으로는 10부봉 데이터 베이스에서 얻은 결과를 가지고서 한번 period 별로 나온 결과에 대해서 한번 이야기를 해 보고자 합니다. 일단 여기서는 어찌된 것인지 period가 증가해도 별로 이익의 평균이 증가하지 않다가 그만 10 period에 가서 급격히 줄어드는 경향을 보이고 있습니다. 아무래도 거래가 잘 일어나지 않은 것이 결정적인 듯 합니다.

그리고 나서 다음으로 표준편차에 4배수를 해주는 조건으로 한번 작업을 해서 비교해 보고자 합니다. 여기서도 역시 이익의 평균은 거의 변화가 없다가 마지막에 가서 거의 0에 수렴할 정도로 급격히 낮아지는 것을 확인할 수 있었습니다. 거의 3배수 이상의 매도/매수 조건은 이 이동평균선 & 표준편차 전략에서 거의 의미가 없는 듯 합니다.

이제 평균은 다 보았으니, 이익과 손해의 합게에 대해서 한번 알아 보고자 합니다. 여기서 뭐랄까, period가 줄어들면 줄어들 수록 표준편차에 배수를 안 주는 조건에서는 이익과 손해의 합계를 보니, period가 줄어들면 줄어들 수록, 이익의 총량은 급격히 증가하고 손해의 총량은 완만하게 줄어들고 있습니다.

이제 표준편차에 2배수를 해준 결과에서 한번 작업을 해 보고자 합니다. 일단 여기서는 이익은 이전 그래프에 비해서 다소 기울기가 완만해 진 감이 있지만, period가 감소할 수록 분명히 증가하고 있고, 손해는 더 가파르게 감소하는 추세를 보이고 있습니다.
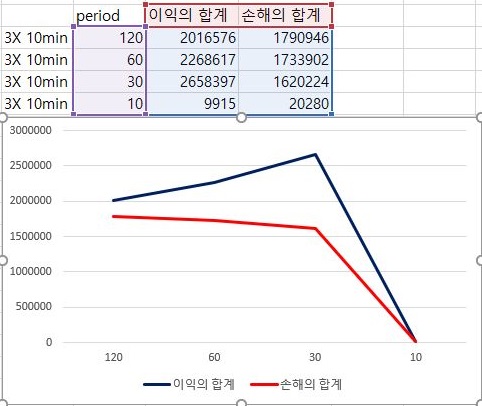
이제 표준편차에 3배수를 해주는 조건을 한번 살펴보도록 하는데, 여기서 나오는 조건을 한번 보자면, 10 period에 가면서 급격히 이익과 손해의 총량이 줄어드는 경향을 보이고 있습니다.

결국 마지막으로 표준편차에 4배수를 해주는 조건을 가지고 실험을 해 보았는데, 여기서 나오는 조건에서 보면, 거의 이익과 손해의 총량이 같다는 것을 알 수 있습니다. 사실상 거의 3배수 이상 부터는 사용이 불가능할 뿐더러, 거의 10period를 사용하는 것이 좋지만, 문제는 이익이 나오는 종목만 골랐는데, 이게 언제까지 수익을 보장해 줄 것이냐 하는 것 입니다.
'무모한 도전-주식 인공지능 만들기' 카테고리의 다른 글
| RSI지수와 새 데이터 분석법 -2- (0) | 2020.04.22 |
|---|---|
| RSI지수와 새 데이터 분석법 -1- (0) | 2020.04.22 |
| 이동평균선과 표준편차의 새 데이터 분석 -4- (0) | 2020.04.20 |
| 이동평균선과 표준편차의 새 데이터 분석 -3- (0) | 2020.04.20 |
| 이동평균선과 표준편차의 새 데이터 분석 -2- (0) | 2020.04.19 |



