안녕하세요?
이번 포스팅에서는 지금까지의 분석만으로도 어느정도 충분할 수 있지만, 한번 30분봉 캔들챠트 데이터 베이스를 이용해서 만든 결과를 비교해 보고자 합니다. 어떤 면에서는 불필요할 수도 있지만, 그래도 한번 비교해 봐야 겠다는 생각이 들어서 포스팅으로 만들어 올리고자 합니다.

일단 위 스크린샷에서 볼 수 있는 것처럼 우선 30분봉 캔들 챠트를 이용해서 나온 결과만을 모아서 비교하도록 도표로 만들어 보았습니다.

일단 평균수익과 표준편차를 비교한 그래프를 그려 보았습니다. 여기서 나오는 그래프를 비교해 보면, 평균수익이 평균과 표준편차를 계산하기 위해서 사용된 분봉의 갯수가 많아지면 많아질 수록 더 떨어지는 것을 확인할 수 있습니다.

그리고 나서 손해를 보는 종목의 갯수는 점점 많아지고, 이익을 보는 종목의 갯수는 줄어드는 현상 역시 관측이 가능하다는 것을 확인할 수 있었습니다.
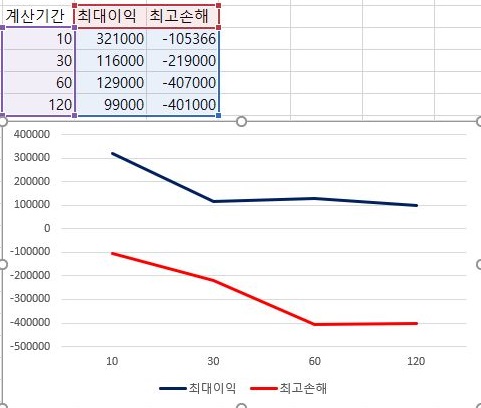
그리고 나서 다음으로 이익의 최대치와 손해의 최대치를 한번 비교해 보았습니다. 역시나 계산에 동원된 분봉의 갯수가 많으면 많을 수록, 표준편차에 1배수를 해준 경우에는 이익은 줄어들고, 손해는 커지는 것을 확인할 수 있었습니다.

그리고 나서 다음으로 해야 할일은 이제 표준편차에 2배를 해서 결과를 얻었는 결과를 한번 비교해서 분석하기 위한 표를 먼저 작성했습니다.

무언가 30분봉 캔들 챠트를 이용한 경우에는 더 심각하다면 더 심각한 것이 일단 매도/매수 룰의 계산에 동원된 분봉의 갯수가 많으면 많을 수록 결과가 더 좋지 않지만, 그 평균수익의 수치가 더 떨어졌다는 것 입니다. 즉, 무언가 상황이 10분봉을 사용한 경우보다 더 좋지 않다는 것을 확인할 수 있습니다.
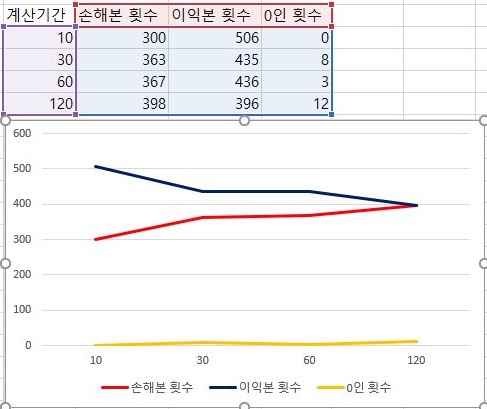
그리고 손해를 본 종목의 갯수와 이익을 본 종목의 갯수를 비교해 보니, 일단 이익을 본 종목은 줄어들고, 손해를 본 종목은 증가를 한다는 것을 확인할 수 있었습니다.
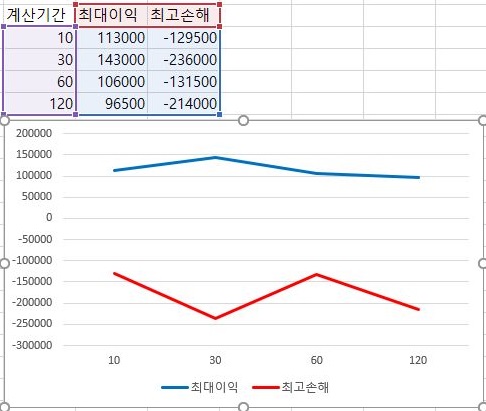
그리고 나서 이익의 최대치와 손해의 최대치를 비교해 보았는데, 그 결과가 그렇게 무어라 말하기 좋지는 않아 보입니다. 일단 이익의 최대치는 그렇게 큰 변화가 안 보이지만, 그렇다고 해서 손해가 더 커지거나 작어지는 경향이 보이지는 않습니다.
'무모한 도전-주식 인공지능 만들기' 카테고리의 다른 글
| 60기간으로 RSI지수 기반 매도/매수 룰 테스트 -1- (0) | 2020.03.16 |
|---|---|
| 평균과 표준편차를 이용한 매도/매수 룰의 정리 -complete- (5) | 2020.03.16 |
| 평균과 표준편차를 이용한 매도/매수 룰의 정리 -2- (0) | 2020.03.16 |
| 평균과 표준편차를 이용한 매도/매수 룰의 정리 -1- (0) | 2020.03.15 |
| 60기간 평균과 표준편차의 결과분석 -3- (0) | 2020.03.15 |



