안녕하세요?
지난번 포스팅에서는 그렇게 결과가 시원치 않음을 어떻게 이야기를 하고나서 끝을 맺었습니다. 그래도 일단 이 결과라도 한번 어느 정도의 데이터 베이스 분봉 간격간 차이가 있는지, 즉 데이터 베이스의 종류에 따라서 어떤 변화를 보여주었는지에 대해서 한번 알아보고자 합니다.

먼저 1배수일때 한번 데이터 베이스의 차이에 따라서 어떤 차이가 나오는지 살펴 보았습니다. 그리고 그 결과가 위 스크린샷과 같은데, 일단 분봉간의 간격이 더 커지면 커질수록 수익이 급격히 떨어지는 것을 확인할 수 있었습니다.
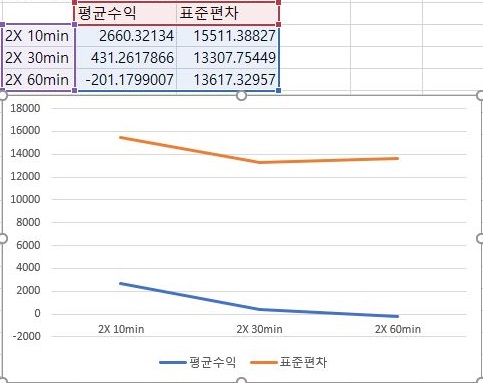
그리고나서 2배수를 한번 살펴 보았는데, 여기서는 더 심각하게도 그나마 10분봉 데이터 베이스를 사용할 경우에나 희망이 있지, 나머지 경우는 답이 없을 수준으로 수익이 하강하는 것을 볼 수 있습니다.
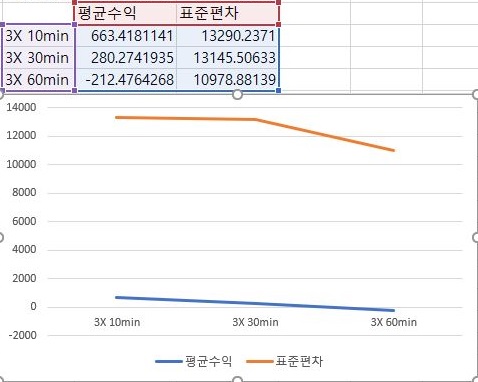
그리고 3배수에 이르러서도 상황은 거의 나아지지 않았습니다. 일단 60개 분봉을 가지고서 매수/매도 룰을 지정했는데, 이게 그렇게 효과가 있는 것은 아닌 것 같습니다.
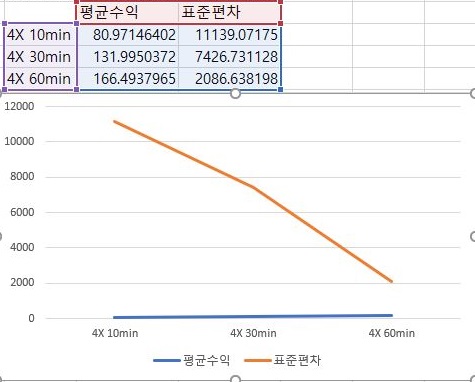
그리고 4배수에 이르러서는 데이터 베이스를 비교하는 것이 거의 의미가 없을 수준으로 수익이 바닥을 기고 있는 것을 확인할 수 있습니다. 이래서야 이걸 활용할 여지가 있는지 의문입니다.
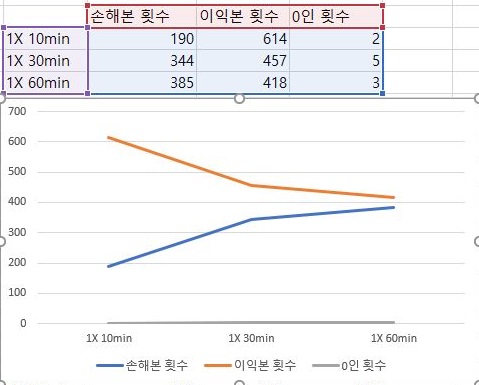
이제 손해를 본 종목의 갯수와 이익을 본 종목의 갯수를 한번 확인해 볼 시간인데, 일단 분봉의 간격이 넓어지면 넓어질 수록, 상황이 더 좋지 않아 진다는 것을 확인할 수 있습니다.

2배수 표준편차에서는 아예 위 스크린샷과 같이 마지막 60분봉을 기준으로 해서 결론을 내릴 경우에는 아예 이익과 손해의 갯수가 역전이 되는 것을 볼 수 있습니다.

그리고 나서 3배수의 경우로 넘어가면, 일단 60분봉을 사용한 경우에 한해서 손해의 양이 줄어드는 것을 볼 수 있지만, 문제는 거래가 없는 경우가 상당히 늘어나기 시작합니다.

그리고 나서 다음으로는 4배수에서 슬슬 거래가 전혀 없는 종목의 갯수가 폭발적으로 60분봉을 쓰면서 늘어나는 것을 볼 수 있습니다.
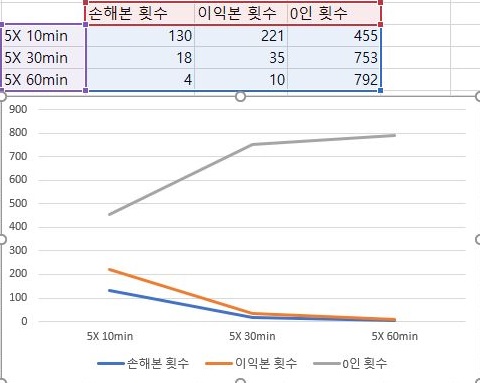
결국 배수를 5배수까지 올리자, 더 이상은 의미가 없다는 말을 하듯이 일단 거래가 전혀 없는 경우가 너무나도 많이 늘어나는 것을 볼 수 있었습니다. 이렇게 해서 결국 10분봉을 사용해야 되는 이유를 더 확실하게 알 수 있었고, 이제는 이 조건을 바탕으로 분봉을 사용한 기간간에 비교가 필요하다는 생각이 들었습니다.
'무모한 도전-주식 인공지능 만들기' 카테고리의 다른 글
| 평균과 표준편차를 이용한 매도/매수 룰의 정리 -2- (0) | 2020.03.16 |
|---|---|
| 평균과 표준편차를 이용한 매도/매수 룰의 정리 -1- (0) | 2020.03.15 |
| 60기간 평균과 표준편차의 결과분석 -2- (0) | 2020.03.15 |
| 60기간 평균과 표준편차의 결과분석 -1- (2) | 2020.03.15 |
| 30기간 평균과 표준편차의 결과분석 -2- (0) | 2020.03.14 |



