안녕하세요?
이번 포스팅에서는 지난번에는 10개의 분봉을 가지고서 평균과 표준편차를 만들어 냈으면, 이번에는 30개의 분봉을 가지고서 평균과 표준편차를 만들어 내는 조건에서 다양한 표준편차 배수를 가지고서 테스트를 했는 결과를 가지고서 한번 분석해 보는 포스팅을 가질까 합니다.

먼저 위 스크린샷에서 볼 수 있는 것처럼, 일단 모든 코스피의 종목에서 이익이든 손해를 최종적으로 보았는 자료를 가지고 와서, 이를 한번 정리해 봅니다.

그렇게 해서 먼저 10분봉 캔들챠트 데이터 베이스에서 얻은 결과를 가지고서, 한번 작업에 들어가 보도록 합니다. 일단 최종결과만을 정리해 보기는 보았습니다.
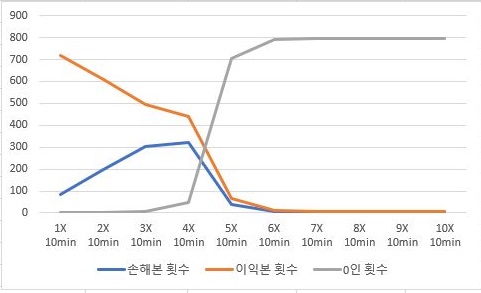
그렇게 해서 일단 손해를 본 종목의 갯수, 이익을 본 종목의 갯수, 그리고 아무런 거래가 없는 종목의 경우의 갯수까지 한번 비교를 해 보고자 합니다. 일단 1배수의 경우가 여기서는 가장 좋은 듯 합니다.

그리고 나서 최대로 얻은 이익과 제일 크게 난 손해량을 비교해 보는 그래프를 그렸습니다. 여기서 나오는 그래프를 보면, 일단 1배수가 가장 좋은 결과를 낸것 같고, 그 이후로는 그렇게 똑 부러지는 것이 없다가 6배수 이상은 더 이상은 볼 필요가 없어졌습니다.

그리고 나서 표준편차를 줄이는 것도 시원치 않았습니다. 그리고 나서 평균수익은 3배수를 넘어가는 시점부터 엄청나게 0에 수렴하는 것을 볼 수 있습니다. 결국 10분봉을 사용하는 경우에는 그냥 1배수를 가지고서 작업에 들어가는 것이 유리해 보입니다.

그리고 나서 30분봉 캔들 데이터 챠트를 가지고서 한번 나왔는 결과를 모아 보았습니다. 이렇게 해서 나온 결과를 바탕으로 해서 한번 작업에 또 들어가 보고자 합니다.

여기서도 1배수의 경우가 가장 이상적으로 나오는 것을 확인할 수 있었습니다. 그리고 나서 다음으로 나오는 것이라면, 역시 4배수를 넘어가는 시점에서 부터는 너무 많은 종목이 거래가 없는 경우가 나오기 때문에, 거의 가치가 없어지는 것을 확인할 수 있었습니다.

그리고 나서 나오는 최대이익과 제일 크게 본 손해의 간극을 한번 재어봤습니다. 일단 어찌된 것인지 이익은 그다지 뾰족하게 경향이 나오지 않았지만, 손해는 3배수때까지 계속해서 증가하는 것을 볼 수 있었습니다.

마지막으로 평균수익과 표준편차를 한번 비교해 보았습니다. 그런데 이렇게 해서 나오는 것을 비교해 보았어도, 문제는 제대로 뭐가 나오지 않는 다는 것을 볼 수 있었습니다. 결국 30분봉 캔들 데이터 베이스를 사용한다고 해도, 역시 1배수를 가지고서 매도/매수의 룰을 형성하는 것이 좋겠다는 생각이 들었습니다.

다음으로는 60분봉 캔들 챠트를 가지고서 한번 평균과 표준편차를 이용한 매도/매수 룰을 테스트 해본 결과를 정리해 보았습니다.

이 경우에는 일단 1배수가 가장 이상적이어 보이기는 합니다만, 2~3배수 사이도 연구해 볼 가치가 있어는 보입니다. 다만, 그걸 감안해도 역시 1배수의 경우가 가장 무난해 보입니다.
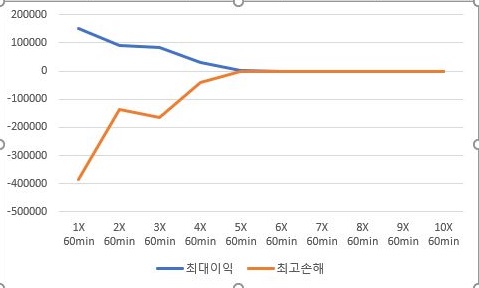
그리고 특이하다면 특이하게도, 손해량 역시 배수가 커지면서 줄어들지만, 문제는 이익량이 너무 작아서, 그냥 1배수를 쓰는 것이 그나마 나은 선택이 아닌가 합니다.
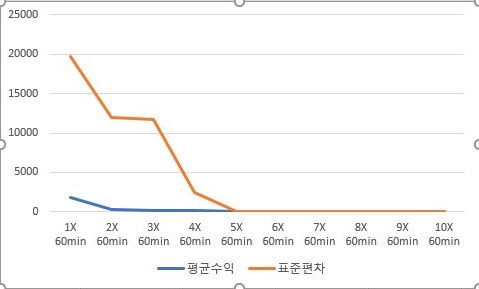
마지막으로 평균수익과 표준편차에 관해서를 살펴보면, 역시나 1배수가 그나마 나은 선택인 것을 확인할 수 있었습니다. 일단 2배수로 넘어 가기만 해도, 수익이 엄청나게 줄어 버리는 것을 보면, 이걸 1배수에서 사용하는 것이 가장 나은 선택이라는 것을 알 수 있었습니다.
'무모한 도전-주식 인공지능 만들기' 카테고리의 다른 글
| 60기간 평균과 표준편차의 결과분석 -1- (2) | 2020.03.15 |
|---|---|
| 30기간 평균과 표준편차의 결과분석 -2- (0) | 2020.03.14 |
| 10기간 평균과 표준편차의 결과분석 -6- (0) | 2020.03.14 |
| 10기간 평균과 표준편차의 결과분석 -5- (0) | 2020.03.14 |
| 10기간 평균과 표준편차의 결과분석 -4- (0) | 2020.03.13 |



